Computational Intelligence: Synergies of Fuzzy Logic, Neural Networks and Evolutionary Computing

Appendix C

MATLAB® Programs for Fuzzy Systems

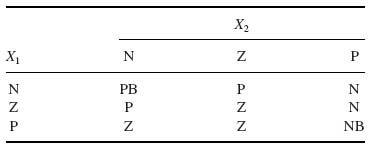
Example C.1.1 A system is described by two inputs (X1, X2) and a single output (Y) within the universes of discourse − 10 ≤ X1 ≤ 10, − 30 ≤ X2 ≤ 30 and − 20 ≤ Y ≤ 20, respectively. In order to develop a Mamdani-type fuzzy system, the membership functions for (X1, X2) and (Y) are defined in Figure C.1.1. The rule base for the Mamdani-type fuzzy system is given in Table C.1.1.

Figure C.1.1 Input and output membership functions. (a) Input membership functions; (b) Output membership function

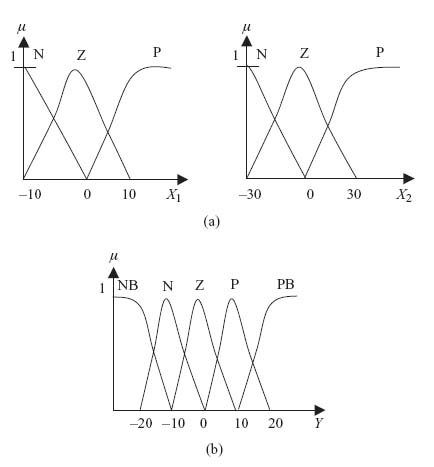
Table C.1.1 Rule base for a Mamdani-type system

A Mamdani-type fuzzy inference system for the above MFs and rule base is developed using MATLAB® and the Fuzzy Logic Toolbox.

 %Fuzzy system − Example C.1.1 clear all;close all; sys=newfis('ExampleFS_1'); %-------------------------Inputs definition ----------------------------- %Define input variable X1 to FIS within interval [-10 10] sys=addvar(sys, 'input', 'X1', [-10 10]); %Define MFs N, Z and P for input X1 sys=addmf(sys, 'input', 1, 'N', 'trimf', [-10 -10 0]); sys=addmf(sys, 'input', 1, 'Z', 'trimf', [-10 0 10]); sys=addmf(sys, 'input', 1, 'P', 'trimf', [0 10 10]); %Define input variable X2 to FIS within interval [-30 30] sys=addvar(sys, 'input', 'X2', [-30 30]); %Define MFs N, Z and P for input ...