Computer Security and Cryptography

12.5 WILLIAMS VARIATION OF RSA

e = 2 is not a permissible exponent in RSA, as the mapping E_e is not one-to-one. The ambiguity in decipherment might be resolved by using a standard format for the plaintext x. It is unlikely, but not proved that only one of the (four) square roots would be in the standard format.

Hugh Williams [1980] found a very clever way around this difficulty. He transforms the plaintext x into E₁[x] where E₁ is an invertible mapping with inverse D₁. For primes with appropriate restrictions, there exist transformations E₂ and D₂ that correspond to encipherment and encipherment such that

The Jacobi symbol J(p/q) when q is a prime is defined by

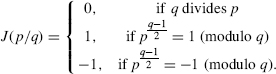
J(p/q) can be extended for q not being a prime.

Proposition 12.8: (Properties of the Jacobi Symbol):

12.8a If p₁ = p₂ (modulo q), then J(p₁/q) = J(p₂/q);

12.8b J(p₁p₂/q) = J(p₁/q)J(p₂/q);

12.8c J(p/q₁q₂) = J(p/q₂)J(p/q₂);

12.8d if p, q are odd; and

12.8e If q is a prime, then .

Proposition 12.9:  If p, q are primes such that 3 = p (modulo 4) = q (modulo 4) and J(x/pq) = 1, then

Proof: Using Proposition 12.8c and the hypothesis ...