Computer Security and Cryptography

2.2 THE RULES OF COLUMNAR TRANSPOSITION ENCIPHERMENT

Columnar transposition (CT) uses a key consisting of

• K1. A (columnar) width N, and
• K2. A transposition τ = (τ₀, τ₁, …, τ_N−1), a permutation of the integers 0, 1, …, N−1.

The encipherment of the plaintext x = (x₀, x₁, …, x_n−1) of length n = (r − 1)N + ℓ ≥ N (0 < ℓ ≤ N) proceeds in two steps:

• CT1. The plaintext x = (x₀, x₁, …, x_n−l) is read by rows into an array X of width N.

  

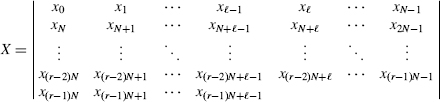
• CT2. The ciphertext y results when X is read out by columns, the order in which the columns are read out being specified by the transposition τ.

The ciphertext is the concatenation of segments corresponding to the columns of X

We use the notation y = T_Nτ(x) to denote that the plaintext x has been enciphered to the ciphertext y by the columnar transposition T_N,τ with key (N, τ).

2.2.1 The Shape of X

If n = (r − 1)N + ℓ with 0 < ℓ ≤ N, then X is a possibly ragged array, where X has¹

1. 
2. A final partial row of ℓ letters, if 0 < ℓ ≤ N;
3. ℓ long columns, each containing 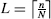letters; and
4. c = n−ℓ short columns, each containing letters.

We write L(j) for the length of the ...