3.8 HILL ENCIPHERMENT OF ASCII N-GRAMS
Monoalphabetic encipherment of N-grams of ASCII plaintext with N > 1 is attractive for two reasons:
- The probability distribution of N-grams with N ≈ 4 is much flatter than for 1-grams, making it harder to recognize letter fragments; and
- There is a very large number 128N of N-grams with N ≥ 4.
Lester Hill [1929] described a simple and elegant way to encipher N-grams of ASCII plaintext. Each character will be identified by its ordinal position in the ASCII character alphabet, integers in ![]() . We suppose the length n of plaintext x = (x0, x1,…, xn−1) is a multiple of N; various modifications are possible when n ≠ kN and will be mentioned later. x is divided into N-grams whose components are integers in
. We suppose the length n of plaintext x = (x0, x1,…, xn−1) is a multiple of N; various modifications are possible when n ≠ kN and will be mentioned later. x is divided into N-grams whose components are integers in ![]() :
:
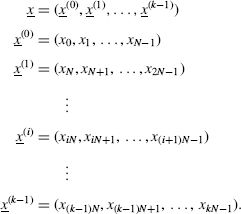
The Hill encipherment of ASCII plaintext x denoted by
![]()
is defined by
![]()
![]()
where
and A = (ai,j) is an N × N matrix with entries in and which is invertible. ...
Get Computer Security and Cryptography now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

