December 2007
Intermediate to advanced
466 pages
10h 6m
English
book
Computing for Numerical Methods Using Visual C++
by Shaharuddin Salleh, Albert Y. Zomaya, Sakhinah A. Bakar
Content preview from Computing for Numerical Methods Using Visual C++
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
Chapter 1. Modeling and Simulation
1.1 Numerical Approximations
1.2 C++ for Numerical Modeling
1.3 Mathematical Modeling
1.4 Simulation and Its Visualization
1.5 Numerical Methods
1.6 Numerical Applications
References
NUMERICAL APPROXIMATIONS
Numerical methods is an area of study in mathematics that discusses the solutions to various mathematical problems involving differential equations, curve fittings, integrals, eigenvalues, and root findings through approximations rather than exact solutions. This discussion is necessary because the exact solutions to these problems are difficult to obtain through the analytical approach. For example, it may be wise to evaluate
Equation 1.1.
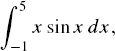
as the exact solution can be obtained through a well-known technique in calculus called integration by parts. However, it is not possible to apply the same method or any other analytical method to solve
Equation 1.2.
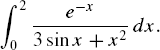
The given equation in the above integral is difficult to solve as it is not subject to the exact methods discussed in ordinary calculus. Therefore, a numerical method is needed to produce a reasonably good approximated solution. A good approximated solution, whose value may differ from the exact solution by some fractions, is definitely better than nothing.
Numerical methods are also needed in cases where ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.