December 2007
Intermediate to advanced
466 pages
10h 6m
English
book
Computing for Numerical Methods Using Visual C++
by Shaharuddin Salleh, Albert Y. Zomaya, Sakhinah A. Bakar
Content preview from Computing for Numerical Methods Using Visual C++
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
Chapter 11. Partial Differential Equations
11.1 Introduction
11.2 Poisson's Equation
11.3 Laplace's Equation
11.4 Heat Equation
11.5 Wave Equation
11.6 Visual Solution: Code11
11.7 Summary
Numerical Exercises
Programming Challenges
INTRODUCTION
Partial differential equation (PDE) is an equation that has one or more partial derivatives as independent variables in its terms. Some typical examples are
Equation 11.1.
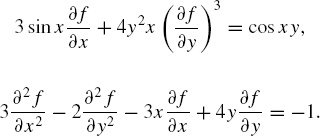
The order of a partial differential equation is defined as the highest partial derivative of the terms in the equation. Therefore, the first example above is the first-order PDE, whereas the second is the second-order PDE. The degree of a partial differential equation is defined as the power of the highest derivative term in the equation. It can be verified from the definition that the two equations above have the degrees of three and one, respectively.
In general, a partial differential equation of order n having m variables x i for i = 1, 2,..., m is expressed as
Equation 11.1.
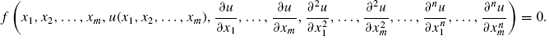
In the above equation,
In this chapter, we will concentrate on numerical problems involving second-order partial differential equations only. A second-order partial differential equation with variables x1, x2, and ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.