Credit Models and the Crisis: A Journey into CDOs, Copulas, Correlations and Dynamic Models

3

Gaussian Copula Model and Implied Correlation

The Gaussian Copula model is a possible way to model the dependence of random variables and, in our case, of default times. As the default event of a credit reference is a random binary variable, the correlation between default events is not an intuitive object to handle. We need to focus our attention rather on default times.

We denote by τ_i the default time of name i in a pool of M names. The default times of different names need to be connected, and the copula formalism allows us to do this in the most general way.

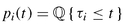
Indeed, if is the default probability of name i by time t, we know that the random variable p_i(τ_i) = U_i is a uniform random variable. Copulas are multivariate distributions on uniform random variables. If we call C(u₁, . . . , u_n) a multivariate uniform distribution, and U₁, . . . , U_M a multivariate uniform with distribution C, then a possible multivariate distribution of the default times with marginals p_i is

(3.1)

where, for simplicity, we are assuming the p’s to be strictly invertible.

Clearly, since the U₁, . . . , U_M variables are connected through a multivariate distribution C, we have a dependence structure on the default times.

The Gaussian Copula enters the picture when we assume that where the X_i are standard ...