Credit Models and the Crisis: A Journey into CDOs, Copulas, Correlations and Dynamic Models

6

A Fully Consistent Dynamical Model: Generalized-Poisson Loss Model

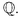
The Generalized-Poisson Loss (GPL) model can be formulated as follows. Consider a probability space supporting a number n of independent Poisson processes N₁, . . . , N_n with time-varying, and possibly stochastic, intensities λ₁, . . . , λ_n under the risk-neutral measure The risk-neutral expectation conditional on the market information up to time t , including the pool loss evolution up to t , is denoted by . 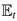Intensities, if stochastic, are assumed to be adapted to such information.

Define the stochastic process

(6.1)

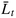
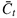
for positive integers α₁, . . . , α_n. In the following we refer to the Z_t process simply as the GPL process. We will use this process as a driving process for the cumulated portfolio loss , the relevant quantity for our payoffs. In Brigo et al. (2006a, 2006b) the possible use of the GPL process as a driving tool for the default counting process is illustrated instead.

The characteristic function of the ...