Credit Risk Modeling Using Excel and VBA with DVD

Appendix A3

Maximum Likelihood Estimation and Newton's Method

The maximum likelihood method is a way of inferring parameter values from sample data. Parameters are chosen such that they maximize the probability (=likelihood) of drawing the sample that was actually observed. We can split the procedure into two main steps:

1. Set up a likelihood function that describes how the probability of a given sample depends on the parameters.
2. Based on step 1, determine the parameters that maximize the likelihood of the sample at hand.

Let us work through a simple example. Consider a sample of three numbers

x₁ = − 1,     x₂ = 5,     x₃ = 2

which are derived from a normal distribution with unknown mean μ and unknown variance σ². The likelihood of observing a single value x_i is given by the density of a normal distribution:

In many cases, we have good reasons to assume that individual draws are independent. The likelihood of the entire data set then can be obtained by multiplying the individual likelihoods. In our case this leads to (recall exp(x)exp(y) = exp(x + y)):

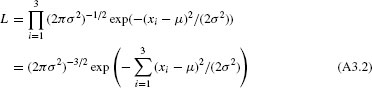
For the simple example, we can easily graph the likelihood function L: it is shown in Table A3.1. The function PI() returns π. To compute the sum of squares ∑(x_i – μ)² we could type (here for cell B8):

($B$2-$A8)^2+($B$3-$A8)^2+($B$4-$A$8)^2 ...