Data Mining, 4th Edition

Appendix A

Theoretical foundations

A.1 Matrix Algebra

Basic Manipulations and Properties

A column vector x with d dimensions can be written

$\mathbf{x}\equiv \left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_d\end{array}\right]={\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_d\end{array}\right]}^T,$

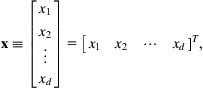
where the transpose operator, superscript T, allows it be written as a transposed row vector—which is useful when defining vectors in running text. In this book, vectors are assumed to be row vectors.

The transpose A^T of a matrix A involves copying all the rows of the original matrix A into the columns of A^T. Thus a matrix with m rows and n columns becomes a matrix with n rows and m columns:

$\begin{array}{ccc}\mathbf{A}\equiv \left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{21}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]& \Rightarrow & {\mathbf{A}}^{\mathit{T}}=\left[\begin{array}{cccc}{a}_{11}& a_{21}& \cdots & a_{m1}\\ a_{12}& a_{21}& \cdots & a_{m2}\\ ⋮& ⋮& \ddots & ⋮\\ a_{1n}& a_{2n}& \cdots & a_{nm}\end{array}\right]\end{array}.$

The dot product