Differential Equations: An Introduction to Modern Methods and Applications, 2nd Edition

Matrices and Linear Algebra

lementary matrix methods were introduced in Chapter 3 to facilitate the study of first order linear systems of dimension 2. In Appendix A, we present several additional concepts and tools from matrix theory necessary for the study of first order linear systems of dimension n ≥ 2 taken up in Chapter 6. Readers with an adequate background in matrix methods and linear algebra may wish to proceed directly to Chapter 6, referring back to this appendix for reference or review if necessary.

A.1 Matrices

The idea of the matrix as a mathematical object is most easily conveyed by considering a type of problem that frequently occurs in science and engineering, the linear algebraic system of equations. For example, consider the system

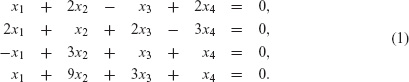
Solving the system (1) means explicitly characterizing the set of all values of x₁, x₂, x₃, and x₄ that simultaneously satisfy all four equations. The solution may simply consist of numerical values for the unknowns, or it may require a mathematical description of a more complex solution set. All information required to solve the problem resides in the coefficients of the unknowns, whereas the names for the unknowns are largely irrelevant. ...