Differential Equations Workbook For Dummies®

2.6. Answers to Separable First Order Differential Equation Problems

Here are the answers to the practice questions I provide throughout this chapter. I walk you through each answer so you can see the problems worked out step by step. Enjoy!

1 Solve this differential equation:

where

y(0) = 5

Solution:

1. First, multiply both sides by dx:

   dy − x³ dx = 0

2. Separate x and y terms on different sides of the equal sign:

   dy = x³ dx

3. Then integrate to get

   

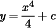
4. Last but not least, apply the initial condition to find that

   c = 5

5. So your answer is

   

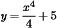
2 Figure out the answer to the following:

where

y(0) = 1

Solution: y = sin (x) + 1

1. Multiply both sides by dx:

   dy − cos (x) dx = 0

2. Then separate x and y terms on opposite sides of the equal sign:

   dy = cos (x) dx

3. Next up, integrate:

   y = sin (x) + c

4. Applying the initial condition tells you that

   c = 1

5. So the solution is

   y = sin (x) + 1

3 What's the solution to this equation?

where

y(0) = 0

Solution: y = x

1. First, multiply both sides by dx:

   y dy − x dx = 0

2. Separate x and y terms ...