9.5. Answers to Solving Differential Equations with Series Solutions Near Singular Points
Following are the answers to the practice questions presented throughout this chapter. Each one is worked out step by step so that if you messed one up along the way, you can more easily see where you took a wrong turn.
1 What are the singular points of this differential equation?
Solution: x1 = 0 and x2 = 0
First, put the equation into the following form:

where
p(x) = Q(x)/P(x)
and
q(x) = R(x)/P(x)
Doing so gives you
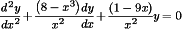
Therefore
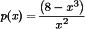
and
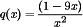
Looks like p(x) and q(x) both become unbounded when x2 = 0, so the singular points are
x1 = 0 and x2 = 0
2 Solve for the singular points of this equation:
Solution: x1 = 9 and x2 = 0
Covert the differential equation to this form:
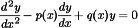
where
p(x) = Q(x)/P(x)
and
q(x) = R(x)/P
Get Differential Equations Workbook For Dummies® now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

