8.3. Exploiting the Power of Power Series to Find Series Solutions
NOTE
Power series are pretty handy for solving ordinary differential equations because you can express just about any solution by using one. When tasked with solving an ordinary differential equation by using a series solution, arm yourself with these essential substitutions:
Substitute this series for y:
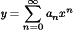
Substitute this series for y′:
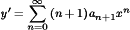
Substitute this series for y″:
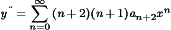
After making these substitutions in your equation, compare the coefficients of x on each side of the equation to solve for the coefficients an in the series terms. (And don't forget to use the initial conditions to solve for the coefficients as well.)
Following is an example of this type of problem with each step worked out. I recommend reviewing it before putting your skills to the test solving ordinary differential equations with series solutions.
NOTE
EXAMPLE
Q. Solve this differential equation by using a series solution:
A. y = a0 cos (x) + a1 sin (x)
Start off with a solution y of the form
To find y″, start by finding y′. Here's what the terms of ...
Get Differential Equations Workbook For Dummies® now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

