Digital Communication Systems

APPENDIX

C  Bessel Functions

C.1   Series Solution of Bessel’s Equation

In a certain class of differential or difference equations encountered in many branches of science and engineering, Bessel functions and their modified versions feature commonly in their solutions, just as cosines and sines feature commonly in trigonometry.

For example, in spectral analysis of analog frequency-modulated (FM) signals (discussed briefly in Chapter 2), the analysis involves the use of Bessel functions of infinite order; see Haykin (2001) for details of this analysis. For yet another example, in studying the Jakes FIR model in Chapter 9 on signaling over fading channels, we found that the Bessel functions of zero order featured in the autocorrelation function at the input of the mobile receiver. Then, in Chapter 7 on signaling over AWGN channels, the modified Bessel function of zero order featured in arriving at the nondata-aided recursive algorithm for symbol timing in the receiver.

These motivating examples prompt us to devote this appendix to mathematical analysis of Bessel functions and their modified versions.

In its most basic form, Bessel’s equation of order n is written as

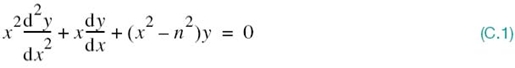
which is one of the most important of all variable-coefficient differential equations. For each n, a solution of this equation is defined by the power series

The function J_n(x) is called a Bessel function of the first ...