Digital Filters Design for Signal and Image Processing

3.6. Frequential characterization of a continuous-time system

3.6.1. First and second order filters

3.6.1.1. 1^st order system

Let us look at a physical system regulated by a linear differential equation of the 1^st order, as is usually the case with RC and LR type filters:

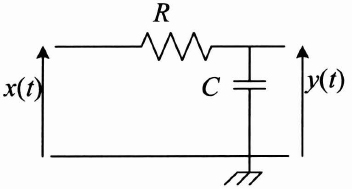
Figure 3.23. RC filter

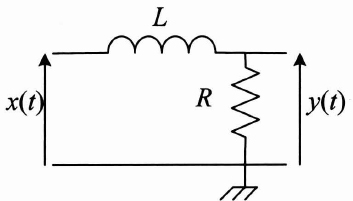
Figure 3.24. LR filter

The transmittance of the system, i.e. , where Y(s) designates the Laplace transform¹ of y(t) and is expressed by:

In taking s = jω where ω = 2πf designates the angular frequency, we obtain:

where K is called the static gain.

With RC and LR filters, the time constant is worth, respectively, τ = RC and and K = 1.

We characterize the system by its impulse response or its indicial response. When x(t) = δ(t), X(s) = 1.

From there:

and if we refer to a Laplace transform table, ...