Digital Filters Design for Signal and Image Processing

8.2. Continuous models

8.2.1. Representation of 2-D signals

In a natural way and as with temporal signals, the usual model for representing two-dimensional signals is the functional model, which can possibly extend to distributions. Since we are most often dealing with images here, temporal coordinates are replaced by spatial coordinates, written as x and y.

Under normal conditions – that is, for finite energy functions – signals can be described in the Fourier domain by means of spatial frequencies u and v, using the bidimensional Fourier transform (FT):

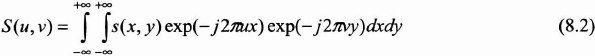
It should be noticed that the 2-D transform is separable. The 2-D calculation is obtained by linking the two calculations of the one dimensional (1-D) transform by successively integrating them in relation to each of the two variables:

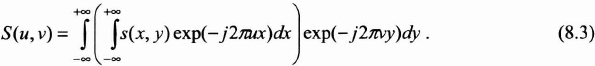
A linear filtering transforms the 2-D signal s(x,y) into another 2-D signal, written here as w(x,y).

Figure 8.1. 2-D linear filtering

The linear filtering operation is represented, In the spatial domain, by the following convolution equation:

It can be described and interpreted in the frequency domain ...