Digital Signal and Image Processing using MATLAB, Volume 1: Fundamentals, 2nd Edition

Chapter 11

Appendix

A1 Fourier transform

Property 11.1 The main properties of the DFT are listed below:

– X(f) is bounded, continuous, tends towards 0 at infinity and belongs to L₂();

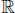
– the Fourier transform is linear;

– expansion/compression of time: the Fourier transform of x(at) is 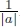X(f/a);

– delay: the Fourier transform of x(t – t₀) is X(f)e^–2jπft₀;

– modulation: the Fourier transform of x(t)e^2jπf₀t is X(f – f₀);

– conjugation: the Fourier transform of x* (t) is X*(–f). Therefore, if the signal x(t) is real, X(f) = X*(–f). This property is said to be of hermitian symmetry;

– if the signal x(t) is real and even, X(f) is real and even;

– if the signal is purely imaginary and odd, X(f) is purely imaginary and odd;

– the convolution product, written (x 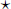y)(t), is defined by:

(11.1)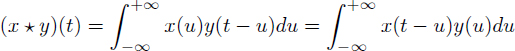

and has X(f)Y(f) as its Fourier transform;

– likewise, the Fourier transform of x(t)y(t) is (X 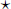Y)(f);

– if x(t) is m times continuously differentiable and if its derivatives are summable up to the m-th order, ...