Digital Signal Processing and Applications with the TMS320C6713 and TMS320C6416 DSK, 2nd Edition

4

Finite Impulse Response Filters

• Introduction to the z-transform
• Design and implementation of finite impulse response (FIR) filters
• Programming examples using C and TMS320C6x code

The z-transform is introduced in conjunction with discrete-time signals. Mapping from the s-plane, associated with the Laplace transform, to the z-plane, associated with the z-transform, is illustrated. FIR filters are designed with the Fourier series method and implemented by programming a discrete convolution equation. Effects of window functions on the characteristics of FIR filters are covered.

4.1 INTRODUCTION TO THE z-TRANSFORM

The z-transform is utilized for the analysis of discrete-time signals, similar to the Laplace transform for continuous-time signals. We can use the Laplace transform to solve a differential equation that represents an analog filter or the z-transform to solve a difference equation that represents a digital filter. Consider an analog signal x(t) ideally sampled,

(4.1)

where δ(t−kT) is the impulse (delta) function delayed by kT and T = 1/F_s is the sampling period. The function x_s(t) is zero everywhere except at t = kT. The Laplace transform of x_s(t) is

(4.2)

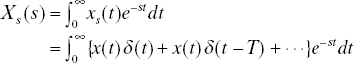
From the property of the impulse function

X_s(s) in (4.2) becomes

(4.3)

Let in (4.3) , which becomes

(4.4)

Let the ...