Digital Signal Processing Using Matlab

1.2. Solved exercises

EXERCISE 1.6.

Define a 4×3 matrix zero everywhere excepting the first line that is filled with 1.

b = ones (1, 3); m = zeros (4, 3); m(1, :) = b
m =
     1   1   1
     0   0   0
     0   0   0
     0   0   0

EXERCISE 1.7.

Consider the couples of vectors (x₁ y₁) and (x₂, y₂). Define the vector x so that:

x(j) = 0 if y₁(j) <y₂(j);

x(j) = x₁(i) if y₁(j) = y₂(j);

x(j) = x₂(j) if y₁(j) > y₂(j)

function x = vectors(x1,y1,x2,y2)
x = x1.*[y1 == y2] + x2.*[y1 > y2];

vectors ([0 1],[4 3], [-2 4] ,[2 0])

ans =
    -2 4

EXERCISE 1.8.

Generate and plot the signal: y(t) = sin(2πt) for 0 ≤ t ≤2, with an increment of 0.01, then undersample it (using the function decimate) with the factors 2 and 16.

t = 0:0.01:2;
y = sin(2*pi*t);
subplot(311)
plot(t,y) ;
ylabel('sin(2.pi.t)');
title('Original signal');
t2 = decimate(t, 2);
t16 = decimate(t2, 8);
y2 = decimate(y, 2);
y16 = decimate(y2, 8);
subplot(312) plot(t2, y2);
ylabel('sin(2.pi.t)')
title('Undersampled signal with a factor 2');
subplot(313);
plot(t16, y16);
ylabel('sin(2.pi.t)');
xlabel('Time t');
title('Undersampled signal with a factor 16');

You can save the figures in eps (Encapsulated PostScript) format, which is recognized by many software programs. The command print -eps file_name creates the file file_name.eps.

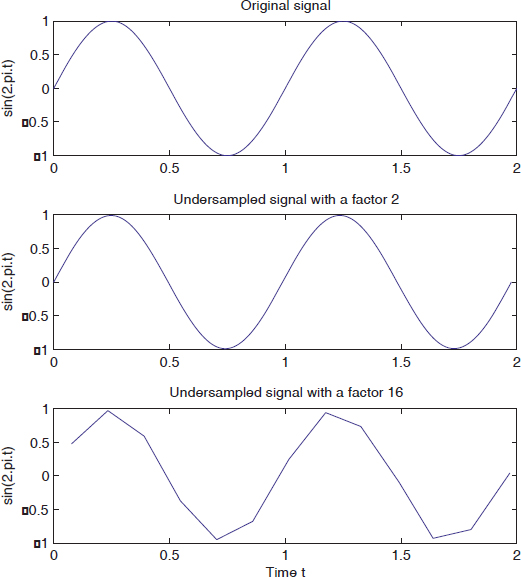
Figure 1.2. Sinusoid waveform corresponding to different sample frequencies

EXERCISE 1.9.

Plot the paraboloid defined by the equation: ...