Digital Signal Processing Using Matlab

5.1. Theoretical background

The discrete Fourier transform (DFT) is a basic tool for digital signal processing. From a mathematical point of view the DFT transforms a digital signal from the original time domain into another discrete series, in the transformed frequency domain. This enables the analysis of the discrete-time signal in both the original and (especially) the transformed domains.

The frequency analyses of a digital filter and of a discrete-time signal are very similar problems. It will be seen in the next chapter that, for a digital filter, it consists of evaluating the transfer function H(z) on the unit circle (z = e^j2πvT). This is the same for the digital signal analysis using the z-transform, which is closely related to the DFT.

As the calculations are performed on a digital computer there are 3 types of errors related to the transition from the Fourier transform of the continuous-time signal to the DFT of the discrete-time signal:

– errors due to time sampling (transition from x(t) to x_s (t)),

– errors due to time truncation (transition from x_s(t) to x_s(t)Π_T(t)),

– errors due to frequency sampling.

5.1.1. Discrete Fourier transform of 1D digital signals

The DFT of finite time 1D digital signals, denoted by DFT_ID, is defined by:

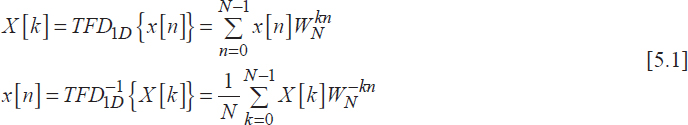
where: W_N = e^−j2π/N and n, k = 0..N –1.

In the above equations, the index of the vectors x[n] and X[k] should begin with 1 instead of 0, ...