Digital Signal Processing Using Matlab

6.1. Theoretical background

A discrete-time system transforms an input digital signal into an output one according to its transfer function. A discrete linear time-invariant system (LTI) can be mathematically described by an operator {x}, so that x → y = {x}, where x and y are the input and output signals respectively.

Digital filtering is one of the most important signal processing functions and the digital filters are the most commonly used LTI. The filtering algorithm can be implemented in the form of a “software solution”, as a routine of a more general program running in the memory of a digital signal processor, or in the form of a “hardware solution”, as a dedicated electronic circuit.

6.1.1. LTI response calculation

The output signal y of a LTI is calculated as the convolution product of its impulse response h with the input signal x, which is considered here as a finite energy signal:

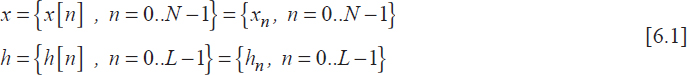
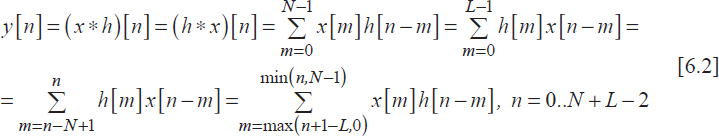
Notice that the output signal y is the sum of partial products obtained through three main operations:

• – time-reversing of the input signal x[-m],
• – time-shifting of the reversed input signal ...