Digital Signal Processing Using Matlab

7.2. Solved exercises

EXERCISE 7.1.

Define in the Laplace domain the transfer function of an anti-aliasing filter, which attenuates with 0.5 dB at the frequency v_p = 3,500 Hz and with 30 dB at the frequency v_a = 4,500 Hz.

Fp = 3500;Fs = 4500;
Wp = 2*pi*Fp; Ws = 2*pi*Fs;
[N, Wn] = buttord(Wp, Ws, 0.5, 30,'s');
[b,a] = butter(N, Wn, 's');
wa = 0: (3*Ws)/511:3*Ws;
h = freqs(b,a,wa) ;
plot (wa/(2*pi), 20*log10(abs(h))) ;grid
xlabel('Frequency [Hz]');
ylabel('Gain [dB]');
title('Frequency response');
axis ([0 3*Fs -60 5]) ;

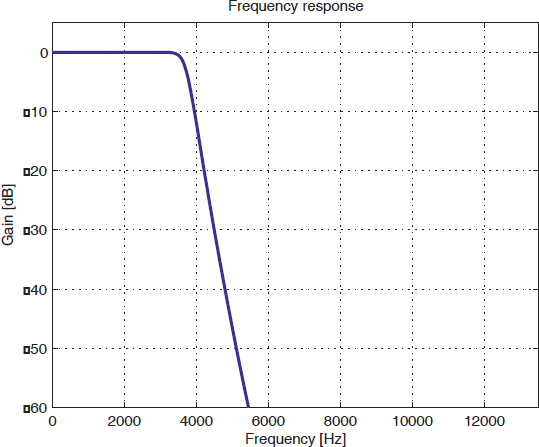
Figure 7.4. Frequency response of an analog Butterworth lowpass filter

EXERCISE 7.2.

Consider a system with the impulse response h[n] = 0.9ⁿ. Plot the impulse response of this system sampled at 1 Hz for values of n between 0 and 50. Demonstrate that its time constant is equal to 10.

n=[0:50]; h=(0.9) .^n;
subplot(211); stem(n,h)
grid; xlabel('n'); ylabel('h(n)')
title('Impulse response')
hI=exp(-n/10);
subplot (212)
plot (n,h1, '+',n,h,'-r')
grid; xlabel('n') ;
legend('exp(-n/10)', 'h(n)')

Figure 7.5. Impulse response of the system from exercise 7.2

The system indicial response can be calculated using the function cumsum.m. The transfer function has a zero in 0 and a pole in 0.9. The impulse and indicial responses can also be calculated using the function filter.m ...