Digital Signal Processing Using Matlab

13.2. Solved exercises

EXERCISE 13.1.

a. Generate and plot three classes of 100 three-dimensional vectors having the mean vectors and the covariance matrices given below:

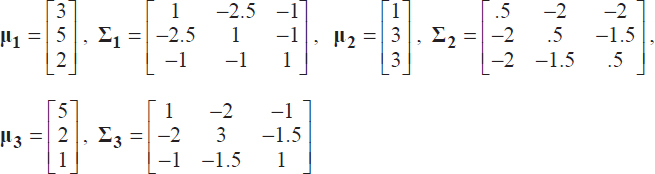
b. Project all these vectors in a two-dimensional space using the principal component analysis. What is the resulting relative error?

c. Perform the linear discriminant analysis on the same vectors' set. Conclude about the interest of this method for better organizing the data before the classification phase.

a.

The following function can be used for generating Gaussian classes:

function matr_gen =
generation_class_gauss(mean_vect,cov_matr,vect_nbr)
% Generation of a Gaussian class
% matr_gen=generation_class_gauss(mean_vect,cov_matr,vect_nbr);
% mean_vect  - mean vector
% cov_matr  - covariance matrix
% vect_nbr - number of vectors
% matr_gen  - matrix of generated vectors
nbre_var=length(mean_vect); matr_init=randn(nbre_var,vect_nbr);
cov_matr_init=cov(matr_init');
matr_transf=real((cov_matr^.5)*(cov_matr_init^-.5));
matr_gen_centered=matr_transf*matr_init ;
matr_gen=repmat(mean_vect,1,vect_nbr)+matr_gen_centered;

The MATLAB code below allows then generating and plotting the three classes:

mean_vect1=[3;5;2]; cov_matr1=[1 -2.5 -1;-2.5 1 -1;-1 -1 1]; mean_vect2=[1;3;3]; cov_matr2=[.5 -2 -2;-2 .5 -1.5;-2 -1.5 .5]; mean_vect3=[5;2;1]; cov_matr3=[1 -2 -1;-2 3 -1.5;-1 -1.5 1]; vect_nbr=100; class1=generation_class_gauss(mean_vect1,cov_matr1,vect_nbr); ...