Direct Eigen Control for Induction Machines and Synchronous Motors

Appendix E

F and G Matrix Calculations

The transition and the input matrix of the discretized state-space equations for the IPM-SM, must be calculated in the (d, q) reference frame, which turns with the rotor, following the rotor magnetic anisotropy, to allow to:

• filter measurements made in the (α, β) fixed frame: the two-phase currents and the position of the rotor, generally
• predict an initial state-space during the control computation.

These two matrices F and G (cf. equations (3.124)) are calculated, from the exponential function of the diagonalized evolution matrix D multiplied by the sampling period T (cf. equation (3.69)), from the input matrix B of the continuous-time state-space equations, and from the transfer matrix and its inverse, calculated in Appendix B and C respectively:

(E.1)    

In addition, the expression of D^{− 1} ⋅ (e^{D ⋅ T} − I) ⋅ P^{− 1} ⋅ B, was already calculated in (3.72).

E.1 Transition Matrix Calculation

We will start by calculating e^{D ⋅ T} ⋅ P^{− 1}, by simply creating the product of the two matrices e^{D ⋅ T} by P^{− 1}, and then we will multiply the result by the matrix P on the left.

(E.2)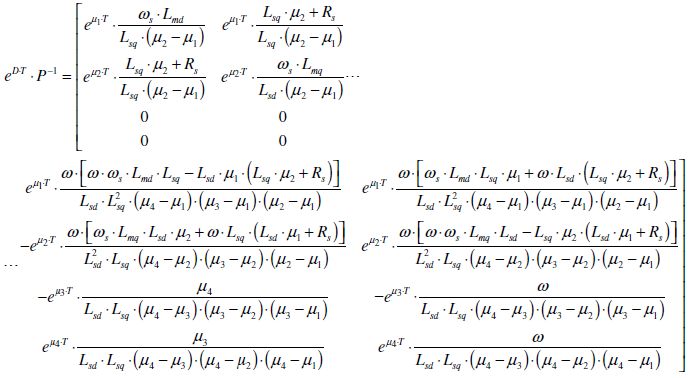    

To reduce the first row of the produced matrix, we then use equations (3.42) and (3.44) and the reduced variable ζ_d1, defined in (3.49). A new relation is thus obtained:

(E.3)    

To reduce ...