12.7 LINEAR TRANSFORMATION
Linear mappings from one vector space to another have acquired an important role in mathematics. Each linear transformation can be represented by a matrix, which enables us to work with the matrix in place of the transformation.
Definition 12.5 Let U and V be vector spaces over the same field F. A mapping T: U → V is said to be a linear transformation if
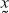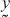- T(
+ 
) = T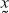 + T, ∀ , ∈ U - T(α) = αT, ∀ α ∈ F, ∈ U
The conditions ...
Get Discrete Mathematical Structures now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
