Chapter 1
Random Vectors
1.1. Definitions and general properties
Recalling that 
the set of real n -tuples, can be fitted into two laws:
making it a vector space of dimension n .
The base implicitly considered on 
n will be the canonical base ℓ1 =(1,0,…0),…,ℓn =(0,…,0,1) and x ∈ n expressed in this base will be denoted:
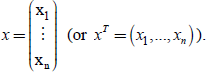
Definition of a real random vector
Beginning with a basic definition, without concerning ourselves for the moment with its rigor: we can say simply that a real vector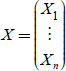 
: linked to a physical or biological phenomenon is random if the value taken by this vector is unknown, as long as the phenomenon is not completed.
For typographical reasons, the vector will instead be written XT =(X1,…,Xn) or even X = (X1,…,Xn) when there is no risk of confusion.
In other words, given a random vector X and B ⊂ n , we do not know if the assertion (also called the event) (X ∈ B) is true or ...
Get Discrete Stochastic Processes and Optimal Filtering, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
