Chapter 2
Gaussian Vectors
2.1. Some reminders regarding random Gaussian vectors
DEFINITION.– We say that a real r.v. is Gaussian, of expectation m and of variance σ2 if its law of probability PX:
– admits the density 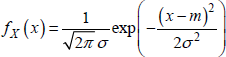 if σ2 ≠ 0 (using a double integral calculation, for example, we can verify that
if σ2 ≠ 0 (using a double integral calculation, for example, we can verify that ![]() ;
;
– is the Dirac measure δm if σ2 = 0.
Figure 2.1. Gaussian density and Dirac measure
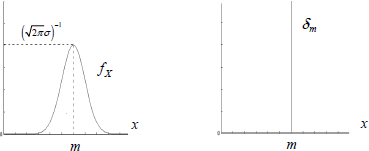
If σ2 ≠ 0, we say that X is a non-degenerate Gaussian r.v.
If σ2 = 0, we say that X is a degenerate Gaussian r.v.; X is in this case a “certain r.v.” taking the value m with the probability 1.
EX = m, Var X = σ2. This can be verified easily by using the probability distribution function.
As we have already observed, in order to specify that an r.v. X is Gaussian of expectation m and of variance σ2, we will write X ~ N(m,σ2).
Characteristic function of X ~ N(m,σ2)
Let us begin by first determining the characteristic function of X0 ~ N(0,1):
![]()
We can easily see that the theorem of derivation under the sum sign can be applied:
Following this, with integration by parts:
The resolution of the differential ...
Get Discrete Stochastic Processes and Optimal Filtering, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

