Discrete Stochastic Processes and Optimal Filtering, 2nd Edition

Chapter 5

The Wiener Filter

5.1. Introduction

Wiener filtering is a method of estimating a signal perturbed by an added noise.

The response of this filter to the noisy signal, correlated with the signal to be estimated, is optimal in the sense of the minimum in L².

The filter must be practically realizable and stable if possible; as a consequence, its impulse response must be causal and the poles inside the circle unit.

Wiener filtering is often used because of its simplicity, but despite this, the signals to be analyzed must be WSS processes.

Examples of applications: word processing, petrol exploration, surge movement, etc.

5.1.1. Problem position

Figure 5.1. Representation for the transmission. h is the impulse response of the filter that we are going to look for

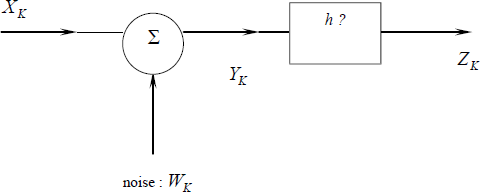
In Figure 5.1, X_K ,W_K and Y_K represent the 3 entry processes, h being the impulse response of the filter, Z_K being the output of the filter which will give _K which is an estimate at instant K of X_K when the filter will be optimal. All the signals are necessarily WSS processes.

We will call:

the representative vector of the process of length N at the input of the realization filter:

– h = (h₀h₁…h_N−1)^T the vector representing ...