2.6. Exercises for Chapter 2
Exercise 2.1.
We are looking at a circular target D of center 0 and of radius R which is used for archery. The couple Z = (X, Y) represents the coordinates of the point of impact of the arrow on the target support; we assume that the r.v. X and Y are independent and following the same law N (0.4R2).
1) What is the probability that the arrow reach the target?
2) How many times must one fire the arrow In order for, with a probability ≥ 0.9, the target is reached at least once (we give ![]() n 10 ≠ 2.305).
n 10 ≠ 2.305).
Let us assume that we fire 100 times at the target, calculate the probability that the target to reached at least 20 times.
Hint: use the central limit theorem.
Solution 2.1.
1) The r.v.s X and Y being independent, the density of probability of Z = (X, Y) is fZ (x, y) = fX (x) fY (y) = 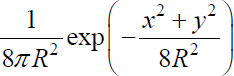 and P (Z ∈ D) =
and P (Z ∈ D) = 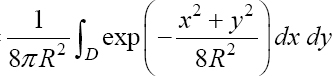 using a change from Cartesian to polar coordinates:
using a change from Cartesian to polar coordinates:
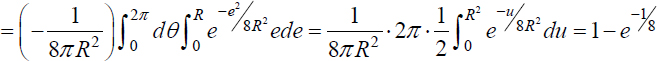
2) At each shot k, we associate a Bernoulli r.v. Uk ∼ b (p) defined by 
In n shots, the number of impacts is given ...
Get Discrete Stochastic Processes and Optimal Filtering now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

