Discrete Stochastic Processes and Optimal Filtering

3.3. Spectral representation of a WSS process

In this section we explain the steps enabling us to arrive at the spectral representation of a process. In order not to obscure these steps, the demonstrations of the results which are quite long without being difficult are not given.

3.3.1. Problem

The object of spectral representation is:

1) To study the integrals (called Wiener integrals) of the type obtained as limits, in a meaning to clarify the expressions with the form:

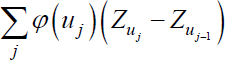
where S is a restricted interval of , φ is a mapping with complex values (and other conditions), Z_S = {Z_u | u ∈ S} is a 2^nd order process with orthogonal increments (abbreviated as p.o.i.) whose definition will be given in what follows.

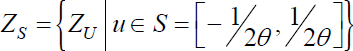2) The construction of the Wiener integral being carried out, to show that reciprocally, if we allow ourselves a WSS process X_θ, we can find a p.o.i. such that ∀j ∈ X_jθ may be written ...