Discrete Stochastic Processes and Optimal Filtering

3.6. Exercises for Chapter 3

Exercise 3.1.

Study the stationarity of the Gaussian process

X ∼ N(m(K), min(j, K)) where E(X_K) = m(K) is constant.

Exercise 3.2.

We are considering the real sequence h_n defined by:

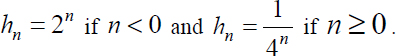
1) Determine the convergence domain of the Laurent series .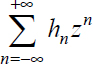

2) If h = {h_n |n ∈ } is a digital filter, determine its transfer function H(z) by clarifying its definition domain.

Solution 3.2.

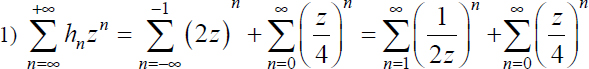
The series converges if and if |z| < 4, thus in the annulus .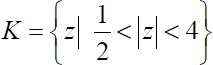

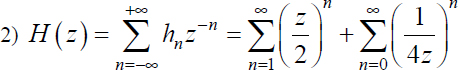
The series converges if |z| > 2 and if |z| < 1/4, thus in the annulus

In K′: .

Exercise 3.3.

Develop H (z)= in series (of Laurent) of ...