4.2. Linear estimation
The fundamental space that we define below has already been introduced in Chapter 3 but in a different context.
DEFINITION.– Space up to instant K − 1 is called linear space of observation and the vector space of the linear combinations of r.v. 1, Y1, …, Yk−1 is denoted ![]() (or
(or ![]() ), i.e.:
), i.e.:
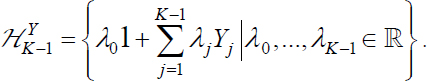
Since r.v. 1, Y1, …, Yk−1 ∈ L2(dP) , ![]() is a vector subspace (closed, as the number of r.v. is finite) of L2(dP).
is a vector subspace (closed, as the number of r.v. is finite) of L2(dP).
We can also say that ![]() is a Hilbert subspace of L2 (dP).
is a Hilbert subspace of L2 (dP).
We are focusing here on the problem stated in the preceding section but with a simplified hypothesis: g is linear, which means that the envisaged estimators Z of XK are of the form:
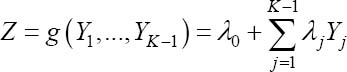 and thus belong to
and thus belong to ![]() .
.
The problem presents itself as: find the r.v., denoted , which renders minimum mapping:
(i.e., find which render minimum: ...
Get Discrete Stochastic Processes and Optimal Filtering now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

