Discrete Stochastic Processes and Optimal Filtering

4.3. Best estimate – conditional expectation

We are seeking to improve the result by considering as estimation of X_K not only the linear functions of r.v. Y₁, …, Y_K−1 but the general functions

PROPOSITION.– The family of r.v. Borel functions; is a closed vector subspace of L².

DEMONSTRATION.–

Let us note again = Hilbert space equipped with a scalar product: .

Furthermore, f_Y (y₁, …, y_{K − 1}) designating the density of the vector Y = (Y₁, …, Y_{K − 1}), in order to simplify its expression let us state:

and let us introduce the new Hilbert space:

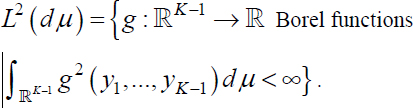
This is equipped with the scalar product: ∀g₁, g₂ ∈ L² (dμ)

Thus finally the linear mapping:

We notice that ψ conserves the scalar product (and the ...