Discrete Stochastic Processes and Optimal Filtering

6.4. Minimization of the cost function

If our system (filter) is linear and non-recursive, we will have a quadratic cost function and this can be represented by an elliptical paraboloid (dim 2) (or a hyperparaboloid if the dimension is superior).

We will call the graphs or same level cost surfaces, i.e. the graphs or surfaces defined vector :

Let us give an example, the equation of the isocosts in the case of a second order filter:

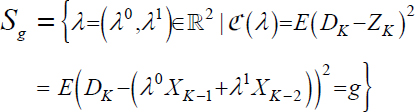
using the stationarity of X_K, we obtain after development the equation of the isocosts

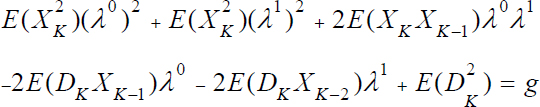
NOTE.– By identification, we easily find the coefficients of the ellipse function of the traditional form:

NOTE.– Still because of the stationarity of X_K, we see that the coefficients arising in the expression of are independent of “K” and this finding is valid for a filter ...