6.6. Geometric interpretation
Let us give another expression to the cost function at instant K.
We have found: 
with 
and 
and Wiener solution of 
.
The cost can be put in the form:
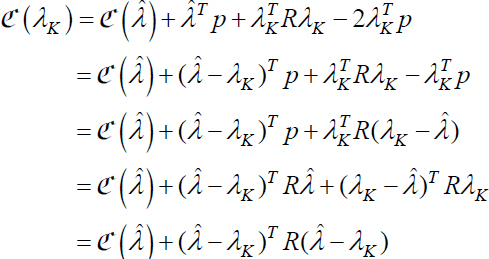
or 
Let us state 
(the origin of the axes is at present 
); it becomes:
and easily: 
: the factor K representing the instant where we are considering the gradient.
Let us simplify the preceding expressions to find simple geometric interpretations by changing the base.
Matrix R being symmetric, we say that it is diagonalizable ...
Get Discrete Stochastic Processes and Optimal Filtering now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
