6.7. Stability and convergence
Let us now study the stability and the convergence of the algorithm of the deterministic gradient.
By taking the recursive expressions of the coefficient vector and by translation:
![]()
The following expressions
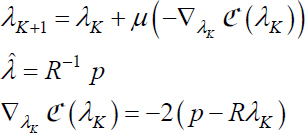
enable us to write: αK+1 = (Id − 2μR)αK Id: identity matrix.
By writing R in the form
![]()
and by premultiplying αK+1 by Q−1, we obtain:
![]()
Thus:
![]()
or: ![]()
and: ![]()
Thus, the algorithm is stable and convergent if
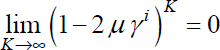
Thus, if and only if ![]()
Thus, if and only if: 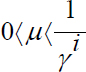
In addition, we ...
Get Discrete Stochastic Processes and Optimal Filtering now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

