Electromagnetism: Maxwell Equations, Wave Propagation and Emission

Answers to Some Problems

Chapter 1

P1.2 a) e′₁ = cos φ e₁ + sin φ e₂, e′₂ = −sin φ e₁ + cos φ e₂, e′₃ = e₃

A′₁ = A₁ cos φ + A₂ sin φ, A′₂ = − A₁ sin φ + A₂ cos φ, A′₃ = A₃

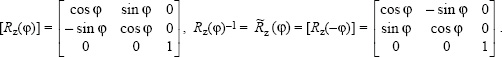
b) B = (μ_oI/2πr′²)(−y′ e′_x + x′ e′_y) is a vector equal to (μ_oI2πr′²)( e′_z × r′), while B′ = (μ_oI/2πr′²) [(x′ sin 2φ + y′ cos 2φ) e′₁ + (x′ cos 2φ − y′ sin 2φ) e′₂] is not a vector.

P1.4 n.E(r) = 4πR²f(R), ∇.E = 2f/r + ∂_rf and ∇.E = 4πR²f(R).

P1.5 Let x′_α = Σ_β R_βα x_β. We find ∂_α = Σ_β ∂′_β.(∂x′ _β/∂x_α) = Σ_β ∂′_β R_αβ = Σ_β R_αβ ∂′_β.

P1.6 b) If dr is on V = Constant, dV = Σ_α ∂_αV dx_α = ∇ V.dr = 0, hence ∇V is normal to dr. c) If only x varies, as r² = x² + y² + z², we get 2r dr = 2x dx, hence ∂_αr = xα/r and ∂_αf(r) = (df/dr)(∂_αr) = (df/dr)(x_α/r). If f = K/r, we find ∂_αf(r) = (−K/r²)(x_α/r) = −Kx_α/r³.

P1.8 a) If V = K(p.r)/r³, E = −∇V = (K/r³)[3(p.r) r/r² − p]. If p = pe_z, V = Kpz/r³ and E = (Kp/r3)[3zr/r² −e_z]. b) If , we find .Using spherical coordinates, if , we find sin θ eφ/r² and .

P1.9 As ∇ × E = 0, E is the gradient of ...