Encyclopedia of Quantitative Finance, IV Volume Set

Galerkin Method see Finite Element Methods

Gamma Hedging

Why Hedging Gamma?

Gamma is defined as the second derivative of a derivative product with respect to the underlying price. To understand why gamma hedging is not just the issue of annihilating a second-order term in the Taylor expansion of a portfolio, we review the profit and loss (P&L)^a explanation of a delta-hedged self-financing portfolio for a monounderlying option and its link to the gamma.

Let us consider an economy described by the Black and Scholes framework, with a riskless interest rate r, a stock S with no repo or dividend whose volatility is σ, and an option O written on that stock.

Let Π be a self-financing portfolio composed at t of

• the option O_t;
• its delta hedge: −Δ_tS_t with 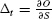; and
• the corresponding financing cash amount −O_t + Δ_tS_t.

We note δΠ the P&L of the portfolio between t and t + δt and we set δS = S_t+δt − S_t. Directly, we have that the delta part of the portfolio P&L is −Δ_tδS and that the P&L of the financing part is (−O_t + Δ_tS_t)rδt. Regarding the option P&L, δO, we have, by a second-order expansion,

Furthermore, the option satisfies the Black and Scholes equation (see Black–Scholes Formula):

Combining ...