Engineering Mathematics, Volume I, Second Edition

6

Tangents and Normals

6.1 INTRODUCTION

We know that a tangent line to a curve C at a point P is the line, in the limiting position, if it exists, of the secant through the point P and a variable point Q on C as Q moves along C closer to P. Also we know that the slope of tangent to the curve y = f (x) at (x, y) is f ′(x).

 

 

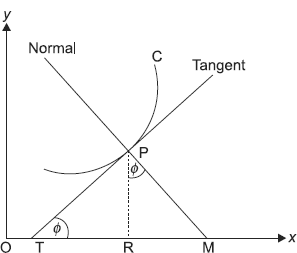
In the figure above, the line P T is tangent to the curve at P, T R is called sub-tangent and RM is called sub – normal.

6.2 EQUATION OF THE TANGENT AT A POINT OF A CURVE

Let P(x₁, y₁) be a point in a curve C. Then equation of a line passing through P(x₁, y₁) and with slope m is given by

 

y – y₁ = m(x – x₁),

where