Engineering Mathematics

2

Mean Value Theorems and Expansion of Functions

Let f be a real-valued function defined on an interval [a, b]. Then, it is said to be derivable at an interior point c if exists. This limit, if exists, is called the derivative or the differential coefficient of the function at x = c and is denoted by f′(c).

The above limit exists, if both the following limits exist and are equal:

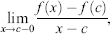1. called the left-hand derivative and denoted by f′(c – 0),
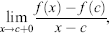2. called ...