13.20 RANK OF A MATRIX
Definition 13.86. A matrix is said to be of rank r if it has at least one non-singular submatrix of order r but has no non-singular submatrix of order more than r.
Rank of a matrix A is denoted by ρ(A).
A matrix is said to be of rank zero if and only if all its elements are zero.
EXAMPLE 13.43
Find the rank of the matrix
Solution. The matrix A is of order 3×4. Therefore, ρ(A) ≤ 3. We note that
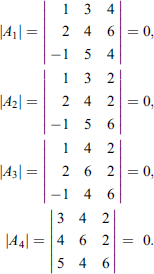
Therefore, ρ(A) ≠ 3. But, we have submatrix , whose determinant is equal to –2 ≠ 0. Hence, by definition, ρ(A) = 2.
EXAMPLE ...
Get Engineering Mathematics now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

