Engineering Mathematics

Case III. Conjugate Complex Roots

1. Suppose that the auxiliary equation has a nonrepeated complex root α + iβ. Then, since the coefficients are real, the conjugate complex number α – iβ is also a non-repeated root. Thus, the solution given in (79) becomes

    

   

    

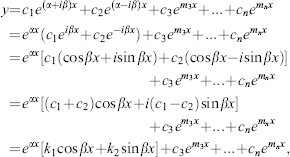
   where k₁ = c₁ + c₂, k₂ = i(c₁ – c₂).

2. If two pairs of imaginary roots are equal, then

    

   m₁ = m₂ = a + iβ and m³ = m⁴ = α – iβ.

    

   Using Case II, the complete solution is

    

   

    

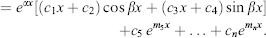
EXAMPLE 15.83

Solve

 

Solution.   The symbolic form of the given equation is

 

(D³ + D² + 4D + 4)y = 0.

 

Therefore ...