Error Correction Coding, 2nd Edition

Chapter 5Rudiments of Number Theory and Algebra

5.1 Motivation

We have seen that the cyclic structure of a code provides a convenient way to encode and reduces the complexity of decoders for some simple codes compared to linear block codes. However, there are several remaining questions to be addressed in approaching practical long code designs and effective decoding algorithms.

1. The cyclic structure means that the error pattern detection circuitry must only look for errors in the last digit. This reduces the amount of storage compared to the syndrome decoding table. However, for long codes, the complexity of the error pattern detection circuitry may still be considerable. It is therefore of interest to have codes with additional algebraic structure, in addition to the cyclic structure, that can be exploited to develop efficient decoding algorithms.
2. The decoders presented in Chapter 4 are for binary codes: knowing the location of errors is sufficient to decode. However, there are many important nonbinary codes, for which both the error locations and values must be determined. We have presented no theory yet for how to do this.
3. We have seen that generator polynomials 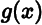must divide 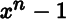. Some additional algebraic tools are necessary to describe how to find such factorizations over arbitrary ...