CHAPTER 17CALCULUS of VARIATIONS
The extremum point of a surface, 
is defined as the point where the first differential, 
vanishes:
Since 
and 
are independent infinitesimal displacements, Eq. (17.1) can only be satisfied when the coefficients of 
and 
vanish simultaneously:
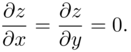
A point that satisfies these conditions is called the stationary point or the extremum point of the surface. To determine whether an extremum corresponds to a maximum or a minimum, one has to check the second differential, 
, which involves second‐order partial derivatives of For a function of independent ...
Get Essentials of Mathematical Methods in Science and Engineering, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
