PART III: PROBLEMS
Section 8.1
8.1.1 Let ![]() = {B(N, θ);0 < θ < 1} be the family of binomial distributions.
= {B(N, θ);0 < θ < 1} be the family of binomial distributions.
8.1.2 Let X1, …, Xn be i.i.d. random variables having a Pareto distribution, with p.d.f.
![]()
0 < ν < ∞ (A is a specified positive constant).
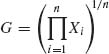 , is a minimal sufficient statistic.
, is a minimal sufficient statistic.8.1.3 Let X be a p–dimensional vector having a multinormal distribution N(μ, ). Suppose that is known and that μ
Get Examples and Problems in Mathematical Statistics now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

