August 2008
Intermediate to advanced
368 pages
7h 54m
English
Content preview from F# for Scientists
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
Chapter 12. COMPLETE EXAMPLES
This chapter details several complete programs that demonstrate some of the most importants forms of scientific computing whilst also leveraging the elegance of the F# language and the power of the .NET platform.
FAST FOURIER TRANSFORM
The program developed in this section combines a core concept in scientific comput-ing with a core concept in computer science:
Spectral analysis: computing the Fourier transform.
Divide and conquer algorithms.
The Fourier transform is one of the most essential tools in scientific computing, with applications in all major branches of science and engineering as well as computer science and even mathematics. This section describes the development of an efficient implementation of the Fourier transform known as the Fast Fourier Transform (FFT).
Discrete Fourier transform
In its simplest form, the Fourier transform
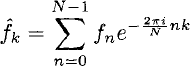
This direct summation algorithm is referred to as the Discrete Fourier Transform (DFT) and is composed of 0(N2) operations, i.e. this algorithm has quadratic asymptotic time complexity.
This naive algorithm may be implemented as a simple F# function:
> #light;; > open System;; > open Math;; > let dft ts = let N = Array.length ts [|for k in 0 .. Array.length ts - 1 -> let mutable z = Complex.zero for n=0 to N-l do let w = 2.0 ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.