Fast Sequential Monte Carlo Methods for Counting and Optimization

Chapter 5

Stochastic Enumeration Method

5.1 Introduction

In this chapter, we introduce a new generic sequential importance sampling (SIS) algorithm, called stochastic enumeration (SE) for counting #P problems. SE represents a natural generalization of one-step-look-ahead (OSLA) algorithms. We briefly introduce these concepts here and defer explanation of the algorithms in detail to the subsequent sections.

Consider a simple walk in the integer lattice . It starts at the origin (0,0) and it repeatedly takes unit steps in any of the four directions, North (N), South (S), East (E), or West (W). For instance, an 8-step walk could be

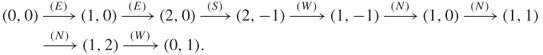
We impose the condition that the walk may not revisit a point that it has previously visited. These walks are called self-avoiding walks (SAW). SAWs are often used to model the real-life behavior of chain-like entities such as polymers, whose physical volume prohibits multiple occupation of the same spatial point. They also play a central role in modeling of the topological and knot-theoretic behavior of molecules such as proteins.

Clearly, the 8-step walk above is not a SAW inasmuch as it revisits point . Figure 5.1 presents an example of a 130-step SAW. Counting ...