Feedback Control for Computer Systems

Appendix C. Complex Numbers

Each complex number z is a point in the complex plane, which is spanned by the real axis and the imaginary axes:

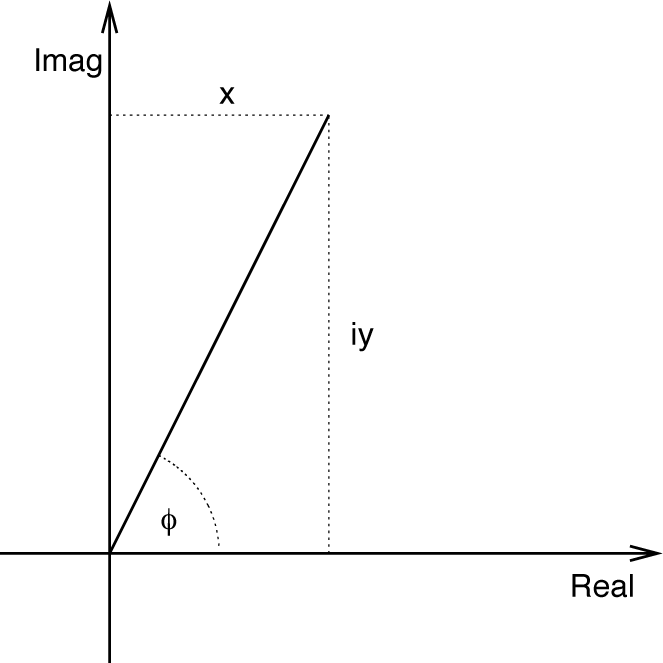
Two coordinate systems are commonly used for a (two-dimensional) plane: Cartesian and polar coordinates. For every complex number there exist two equivalent representations:

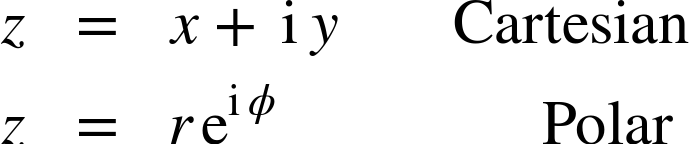
Here

is the “imaginary unit.”

We can transform between those representations as follows:

	Real part
	Imaginary part
	Magnitude
	Phase

Basic Operations

Complex numbers are added and multiplied component by component while taking into account that i² = –1. If z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂, then

z₁ + z₂ = (x₁ + x₂) + i(y₁ + y₂)

z₁z₂ = (x₁x₂ – y₁y₂) + i(x₁y₂ + x₂y₁)

Each complex number z has a “complex conjugate,” denoted , which is the same as except that the sign ...