Fibonacci and Catalan Numbers: An Introduction

Solutions for the Odd-Numbered Exercises

Part One: The Fibonacci Numbers

Exercises for Chapter 4

1. Proof: If not, there is a first integer r > 0 such that gcd (F_r, F_r+2) > 1 . But gcd (F_r−1, F_r+1) = 1. Consequently, there exists a positive integer d, where d > 1 and d divides both F_r and F_r+2. Since F_r+2 = F_r+1 + F_r, it follows that d divides F_r+1. But this contradicts gcd (F_r, F_r+1) = 1, the result in Property 4.1.

3. Proof: F_2(n+1) = F_2n+2 = F_2n+1 + F_2n = (F_2n + F_2n−1) + F_2n = 2F_2n + F_2n−1.

5. Proof: Simply add F_n to each side of the result in Exercise 4.

7. Proof: F_3n = F_3n−1 + F_3n−2 = (F_3n−2 + F_3n−3) + (F_3n−3 + F_3n−4) = F_3n−2 + 2F_3n−3 + F_3n−4 = (F_3n−3 + F_3n−4) + 2F_3n−3 + F_3n−4 = 3F_3n−3 + 2F_3n−4 = 3F_3n−3 + 2(F_3n−3 + F_3n−5) = 3035F_3n−3 − 2F_3n−5 = 4F_3n−3 + (F_3n−4 + F_3n−5) − 2F_3n−5 = 4F_3n−3 + (F_3n−5 + F_3n−6 + F_3n−5) − 2F_3n−5 = 4F_3n−3 + F_3n−6.

9. Proof (By Mathematical Induction): We see that , so the given statement holds in this first case. This provides the basis step of the proof. For the inductive step, we assume the truth of the result for n = k(≥ 0)—that is, that . Now we consider what happens for n = k + 1. In this case, we see that

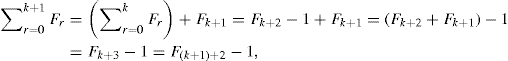
so the truth of the statement at n = k